La risoluzione dell’equazione di secondo grado
Un approccio originale
I Matematici docenti propongono problemi un po’ fuori dalla realtà del tipo:
“Dividi un segmento della lunghezza di 13 𝑚𝑚 in due parti tali che il rettangolo avente per dimensioni queste parti abbia area 36 𝑚𝑚2”
chiedendone la soluzione attraverso la (necessaria) formula risolutiva per l’equazione di secondo grado:
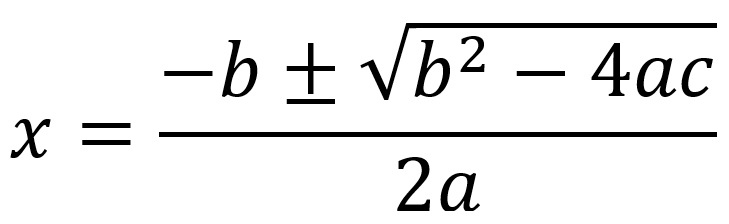
In sintesi, un’equazione di secondo grado è un’eguaglianza tra due espressioni. Nella forma canonica la seconda parte è solamente il valore zero mentre la prima parte è formata da tre elementi (monomi) dei quali due contengono la cosiddetta incognita (che porta ad eguagliare a zero la somma dei tre) rappresentata, per convenzione, ma non obbligatoriamente, dalla lettera “x”. La prima scrittura dell’incognita è elevata al quadrato e tutte e due sarebbero precedute da un coefficiente,
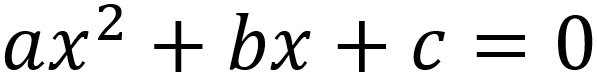
ma una divisione del trinomio per il coefficiente dell’incognita al quadrato (tanto, dall’altra parte dell’eguaglianza, lo zero diviso qualsiasi numero diverso da zero sempre zero rimane)
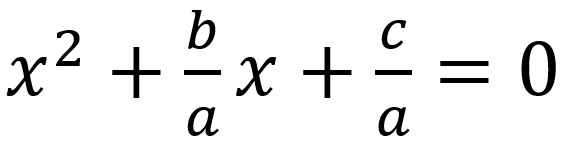
porta ad una forma elegante: l’incognita al quadrato, più (o meno) un po’ di volte l’incognita semplice, più il termine noto danno somma zero
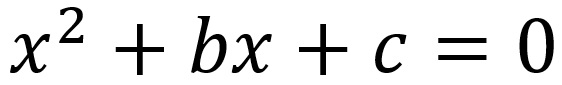
[i parametri sono stati rinominati arbitrariamente]
Dall’equazione di secondo grado scaturiscono due soluzioni che possono essere diverse, coincidenti, oppure costituite da numeri complessi (un numero reale, più o meno un numero immaginario). Basti questo per comprendere che l’equazione (di secondo grado) derivi da una semplice ed ovvia formuletta:
il prodotto dell’incognita meno un certo valore (soluzione uno), per l’incognita meno un secondo valore (soluzione due), dà come risultato (è uguale a) zero
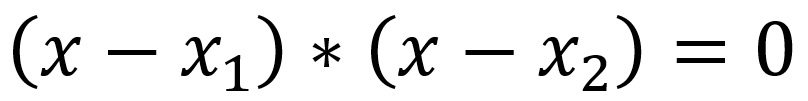
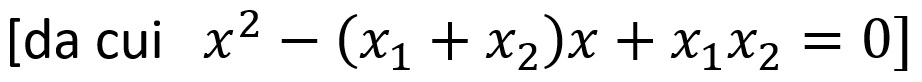
La prova è che se attribuiamo all’incognita il valore della soluzione uno oppure quello della soluzione due, il risultato dell’intera espressione è zero.
Ecco, eseguendo i semplici calcoli su questa formula generatrice, si giunge rapidamente all’espressione canonica dell’equazione di secondo grado con la natura (l’origine) del coefficiente dell’incognita e del termine noto:
l’incognita al quadrato meno la somma delle due soluzioni per l’incognita, più il prodotto delle stesse soluzioni dà come risultato zero
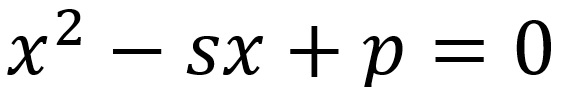
Questo è l’equazione di secondo grado. Come risolverla?
Senza scomodare le biblioteche delle Facoltà di Matematica si viene facilmente a sapere che la trattazione della questione ha nome, date, luoghi e procedimenti illustri: gli antichi babilonesi, in Mesopotamia, con le loro tavolette di argilla, il matematico indiano Baudhāyana, ed il Shulba Sutras nell'antica India all'incirca nell'VIII secolo a.C., i matematici cinesi, ed Euclide, Diofanto di Alessandria, il manoscritto di Bakhshali, scritto in India fra il 200 a.C. e il 400 d.C., che introdusse la formula risolutiva. E poi Brahmagupta (India, VII secolo). Più tardi il grande Al-Khwarizmi (Bagdad, IX secolo d.C). Più “vicino a noi, nel tempo, Abraham bar Hiyya Ha-Nasi (conosciuto anche con il nome latino Savasorda, Barcellona, 1070 – Provenza, 1136). E tanti altri, perfino Cartesio. Ma tutte queste notizie si trovano facilmente nel Web, come a:
https://it.m.wikipedia.org/wiki/Equazione_di_secondo_grado
Almeno per originalità è il caso di osservare che la conoscenza della differenza tra due valori e la loro somma è sufficiente per determinare, intuitivamente e senza percorsi troppo tecnici, quei due valori. Infatti, con un po’ di immaginazione, se siamo esercitati, vediamo chiaramente che la somma dei due, più o meno la differenza tra loro ci consente di giungere proprio a quei due valori.
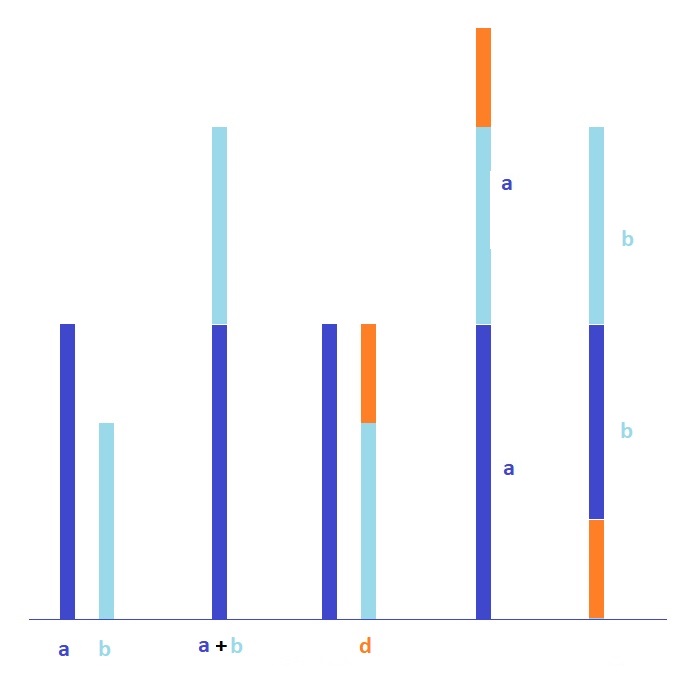
Ci occorre però la differenza tra le due soluzioni mentre noi ne conosciamo la somma: qui viene in nostro soccorso l’Algebra per la quale la differenza tra due monomi al quadrato si ottiene togliendo al quadrato della loro somma quattro volte il loro prodotto.
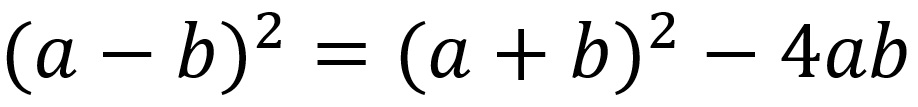
In definitiva, dunque:
le due soluzioni si ottengono aggiungendo o sottraendo alla loro somma la radice quadrata della loro somma al quadrato diminuita di quattro volte il loro prodotto, e dividendo a metà.
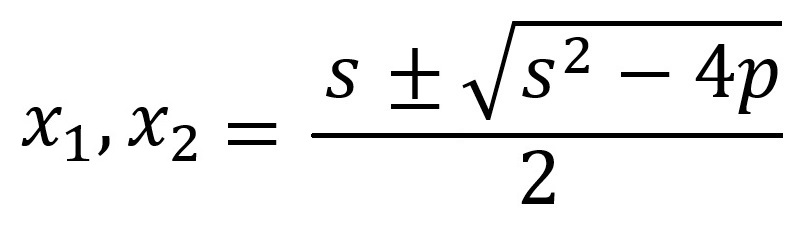
Sarebbe tutto. Ma per completezza possiamo esprimere la stessa definizione nel caso in cui nella equazione di partenza non fosse “uno” ma genericamente “a” il coefficiente dell’incognita al quadrato e che per questo fosse diviso tutto il trinomio precedente il segno “uguale”:

le due soluzioni si ottengono aggiungendo o sottraendo alla metà della loro somma divisa per il coefficiente “a” la metà della radice quadrata della loro somma al quadrato diminuita di quattro volte il loro prodotto anche questa divisa per ”a”:
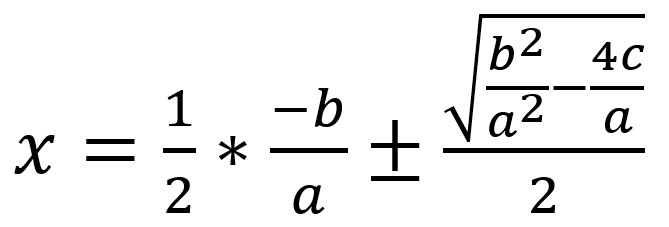
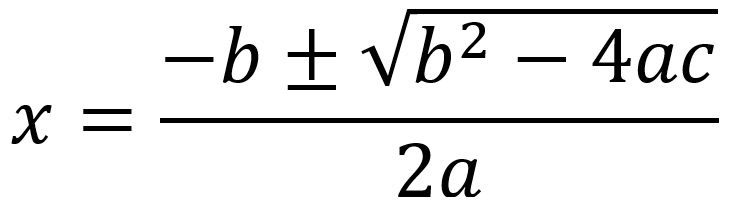
Appendice
A proposito del quadrato di un binomio
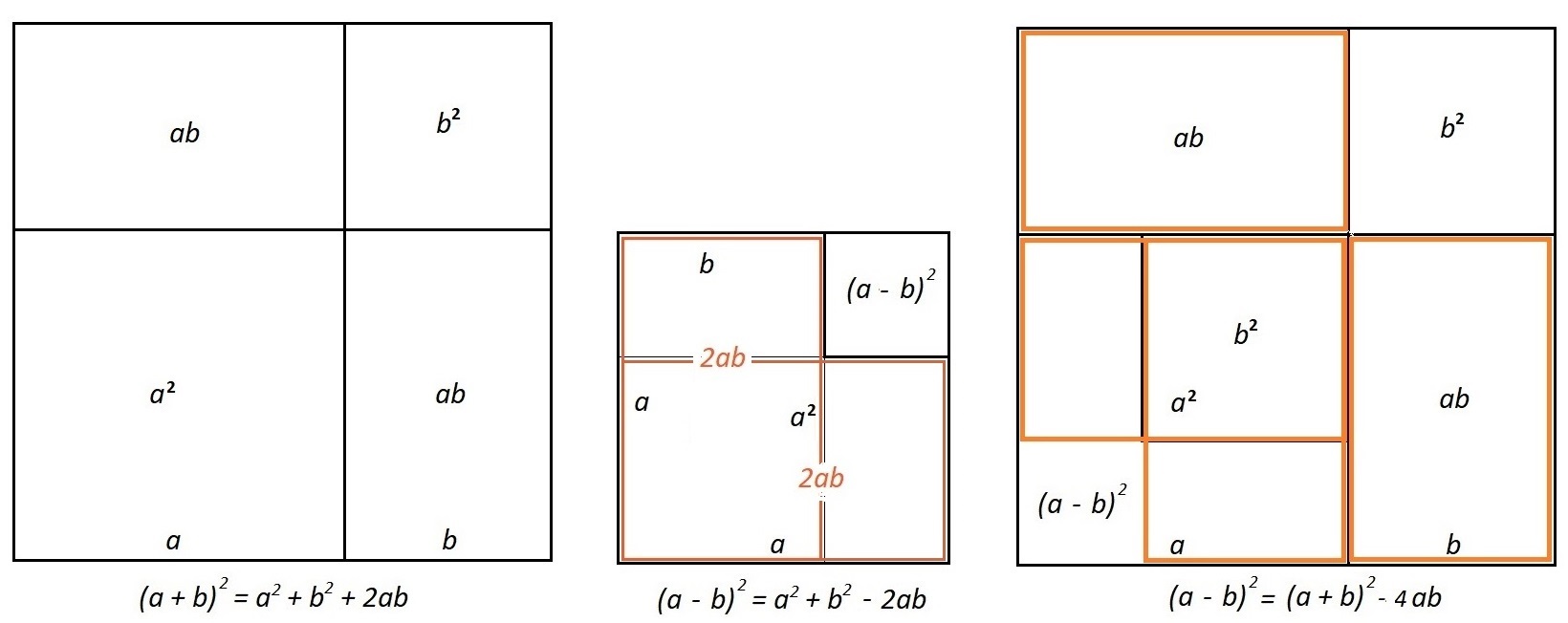
Le prime due figure sono chiare. Per la terza si noti che il quadrato grande (a + b)2 viene diminuito dai quattro rettangoli bordati marrone per i quali un quadrato b2 è sovrapposto e compensato da quello nell’angolo destro, in alto.